Das Kontinuum-Modell ist kompliziert. Es berücksichtigt auch die Wechselwirkung zwischen der Platte und dem Boden. Es stellt den Boden als ein geschichtetes Kontinuum oder isotropes elastisches Halbraummedium dar.
Obwohl das Kontinuum-Modell eine sehr gute Methode zur Erfassung der Baugrundverhältnisse bereitstellt, konnte es früher aufgrund seiner mathematischen Schwierigkeiten nur selten genutzt werden. Die sinnvolle Anwendung des Verfahrens für allgemeine Baugrund- und Bauwerksverhält-nisse verursacht einen relativ großen Rechenaufwand. Deshalb ist die praktische Verwendung ohne Computer nur möglich, wenn entsprechend aufbereitete Tafel- oder Tabellenwerke zur Verfügung stehen. Diese Ta¬bellen sind auf ebene Probleme begrenzt.
Um unabhängig von Tabellen praxisnahe Eingangswerte über den Baugrund und das Bauwerk berücksichtigen zu können, wurde zunächst eine allgemeine, für Computer geeignete mathematische Lösung entwickelt, die auf einem FE-Modell für die Sohlplatte basiert. Damit können Gründungsplatten mit den der Wirklichkeit am nächsten kommenden Baugrundmodellen dargestellt werden. Es können Platten mit beliebiger Grundriss-Form gerechnet werden. Auch können Löcher in der Platte und die Interaktion von Nachbarplatten berücksichtigt werden. Mit dem für diese Zwecke für die Praxis entwickelten Computerprogramm ELPLA kann man mit den weitgehend gleichen Ausgangsdaten verschiedene Typen von Baugrundmodellen anwenden. Es ist auch möglich, beim dreidimensionalen Kontinuum-Modell unregelmäßige Schichtenverläufe zu berücksichtigen. Darüber hinaus kann mit dem Programm ELPLA der Einfluss der Struktursteifigkeit (feldweise veränderliche Dicke der Sohlplatte) auf das System Baugrund/ Bauwerk und der Einfluss von Temperaturänderung auf die Platte dargestellt werden.
1 - Nichtlineare Berechnung unter Verwendung eines
hyperbolischen Funktionsmodells
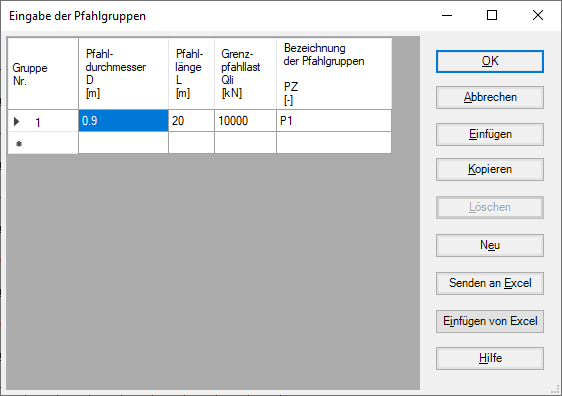
In diesem Modell werden alle auf die Platte einwirkenden Kräfte nichtlinear auf die Pfähle übertragen, wobei die hyperbolische Funktion zur Lastsetzung verwendet wird.
In diesem Modell werden alle auf die Platte einwirkenden Kräfte nichtlinear auf die Pfähle übertragen, wobei die hyperbolische Funktion zur Lastsetzung verwendet wird.
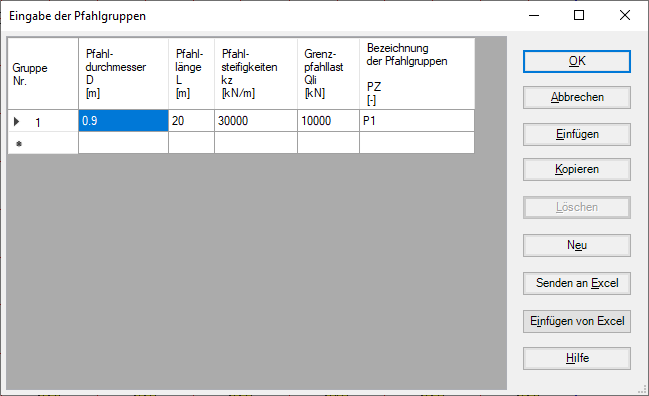
Bild 32 "Eingabe der Pfahlgruppen" Nichtlineare Berechnung mit hyperbolischer Funktion zur Last-Setzung
2 - Nichtlinearen Berechnung nach deutscher Norm DIN-4014
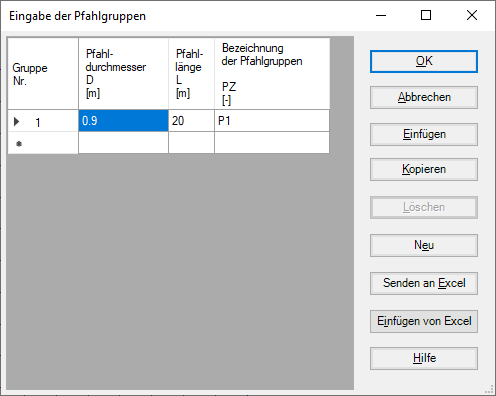
In diesem Modell werden alle auf die Platte einwirkenden Kräfte nichtlinear auf die Pfähle übertragen, wobei die deutscher Norm DIN-4014 zur Lastsetzung verwendet wird.
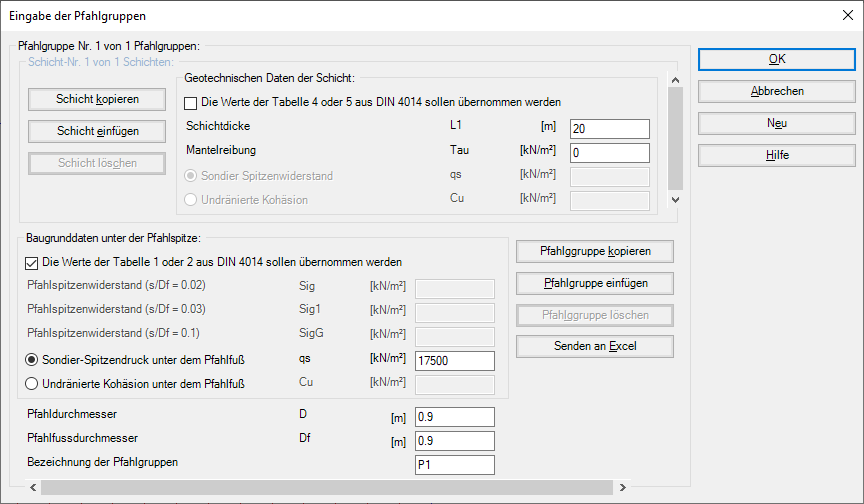
Bild 33 "Pfahlgruppen definieren" Nichtlineare Berechnung nach deutscher Norm DIN-4014
3 - Nichtlinearen Berechnung nach deutschen Empfehlungen EA-Pfähle
In diesem Modell werden alle auf die Platte einwirkenden Kräfte nichtlinear auf die Pfähle übertragen, wobei die deutscher Empfehlungen EA-Pfähle zur Lastsetzung verwendet wird.
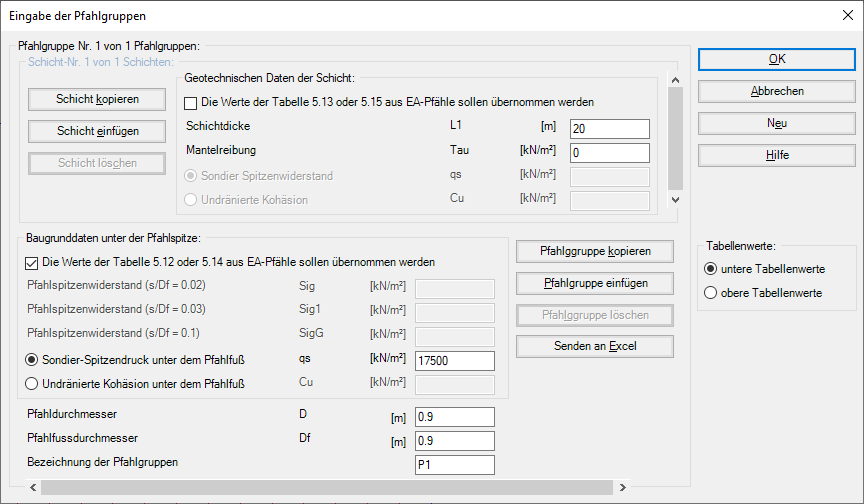
Bild 34 "Pfahlgruppen definieren" Nichtlineare Berechnung nach deutschen Empfehlungen EA-Pfähle
4 - Nichtlineare Berechnung unter Verwendung einer gegebenen Last-Setzungskurve
Last-Setzungskurve
In diesem Modell werden alle auf die Platte einwirkenden Kräfte nichtlinear auf die Pfähle übertragen, wobei unter Verwendung einer gegebenen Last-Setzungskurve zur Lastsetzung verwendet wird. Lastsetzungslinie für Pfahlgruppe und Pfahl-Plattengründung, kann aus zwei Widerstand-Setzung Beziehungen wie folgt erhalten werden:
In diesem Modell werden alle auf die Platte einwirkenden Kräfte nichtlinear auf die Pfähle übertragen, wobei unter Verwendung einer gegebenen Last-Setzungskurve zur Lastsetzung verwendet wird. Lastsetzungslinie für Pfahlgruppe und Pfahl-Plattengründung, kann aus zwei Widerstand-Setzung Beziehungen wie folgt erhalten werden:
a) Mantelwiderstand mit Spitzenwiderstand-Setzung, Bild 36.
b) Pfahlwiderstand-Setzung, Bild 37.
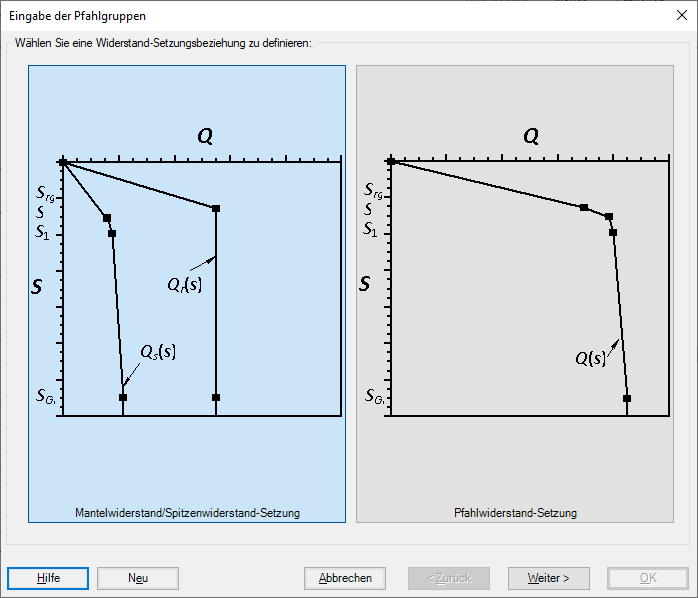
Bild 35 "Eingabe der Pfahlgruppen" Nichtlineare Berechnung unter Verwendung einer gegebenen Last-Setzungskurve
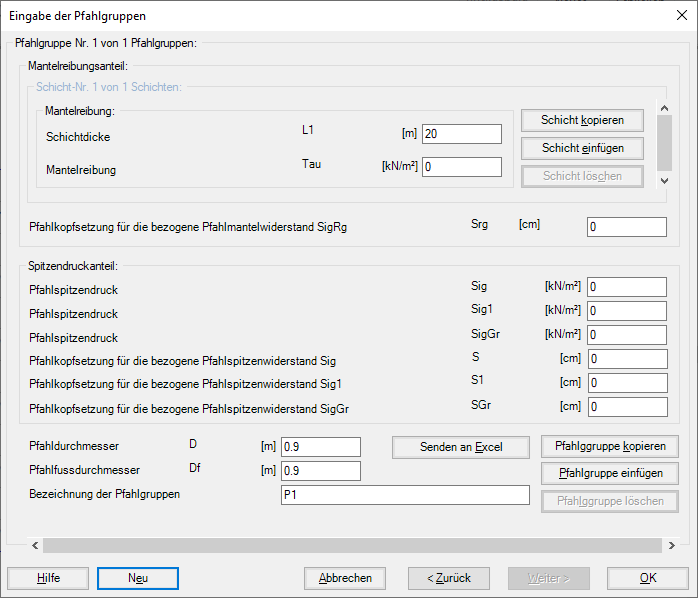
Bild 36 "Eingabe der Pfahlgruppen" Mantelwiderstand mit Spitzenwiderstand-Setzung
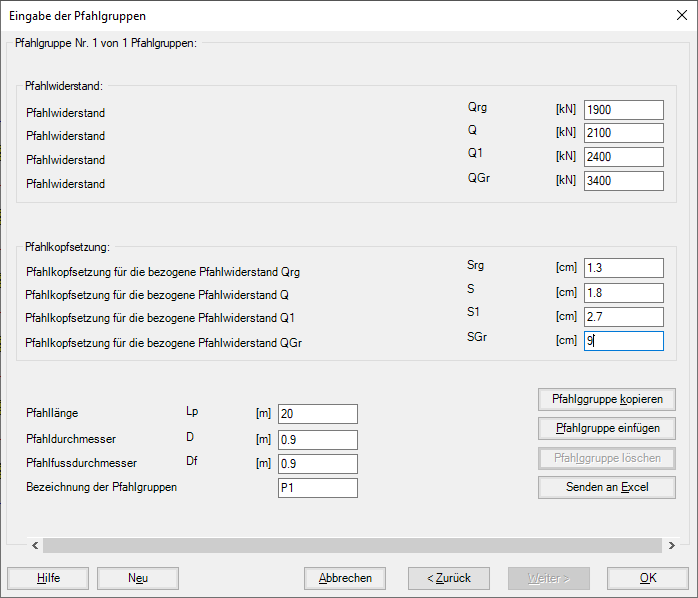
Bild 37 "Eingabe der Pfahlgruppen" Pfahlwiderstand-Setzung